data("EuStockMarkets")
library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
autoplot(EuStockMarkets[,1:2])+ xlab("") + ylab("") + theme_bw()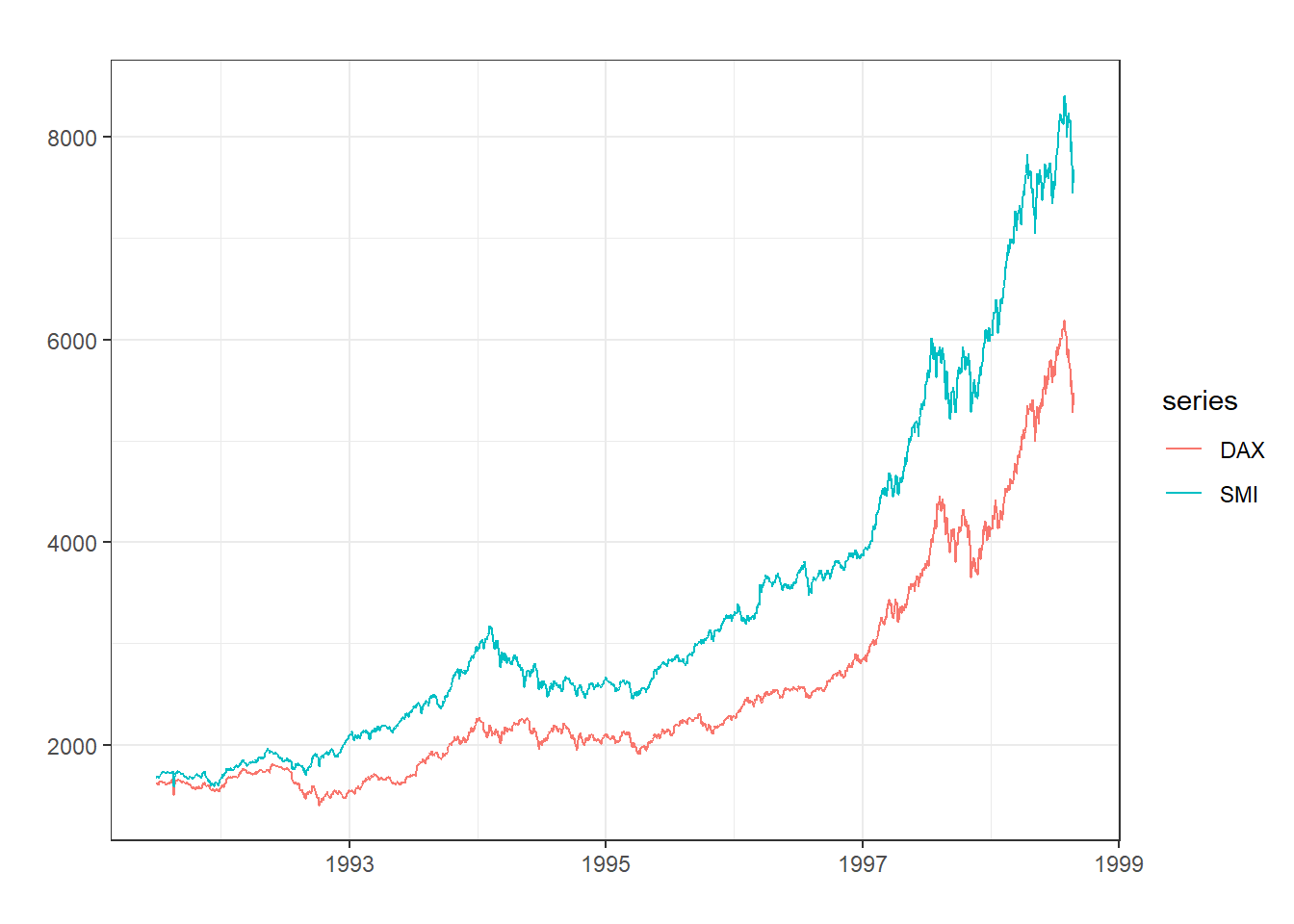
Javier Sánchez García
January 1, 2012
Hasta ahora se ha visto que una serie es estacionaria si es I(0), estacionaria tras realizar primeras diferencias si es I(1), y así sucesivamente hasta I(\(d\) ).
Sin embargo, también es posible que la diferencia entre dos series sea estacionaria:
\[ Z_t = Y_t- \alpha X_t = I(0) \] Este concepto se denomina cointegración, término que denota el que la diferenciación de dos series sea estacionaria. A efectos prácticos, esto implica que las series comueven a largo plazo ya que comparten una tendencia estocástica común. Esto implica que se mueven a la par con desviaciones temporales a corto plazo.
data("EuStockMarkets")
library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
autoplot(EuStockMarkets[,1:2])+ xlab("") + ylab("") + theme_bw()
Es bastante evidente que cuando una serie aumenta, la otra también lo hace y viceversa.
$DAX
KPSS Test for Level Stationarity
data: X[[i]]
KPSS Level = 15.401, Truncation lag parameter = 8, p-value = 0.01
$SMI
KPSS Test for Level Stationarity
data: X[[i]]
KPSS Level = 16.457, Truncation lag parameter = 8, p-value = 0.01reg <- lm(EuStockMarkets[,1] ~ EuStockMarkets[,2], data=EuStockMarkets) #Estimación del parámetro alpha
summary(reg)
Call:
lm(formula = EuStockMarkets[, 1] ~ EuStockMarkets[, 2], data = EuStockMarkets)
Residuals:
Min 1Q Median 3Q Max
-285.75 -106.88 -20.15 104.20 603.45
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.478e+02 7.558e+00 46.02 <2e-16 ***
EuStockMarkets[, 2] 6.465e-01 2.008e-03 321.91 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 144 on 1858 degrees of freedom
Multiple R-squared: 0.9824, Adjusted R-squared: 0.9824
F-statistic: 1.036e+05 on 1 and 1858 DF, p-value: < 2.2e-16z_t = EuStockMarkets[,1] - 6.465e-01*EuStockMarkets[,2] #Serie conjunta
autoplot(z_t) + theme_bw() #Análisis visual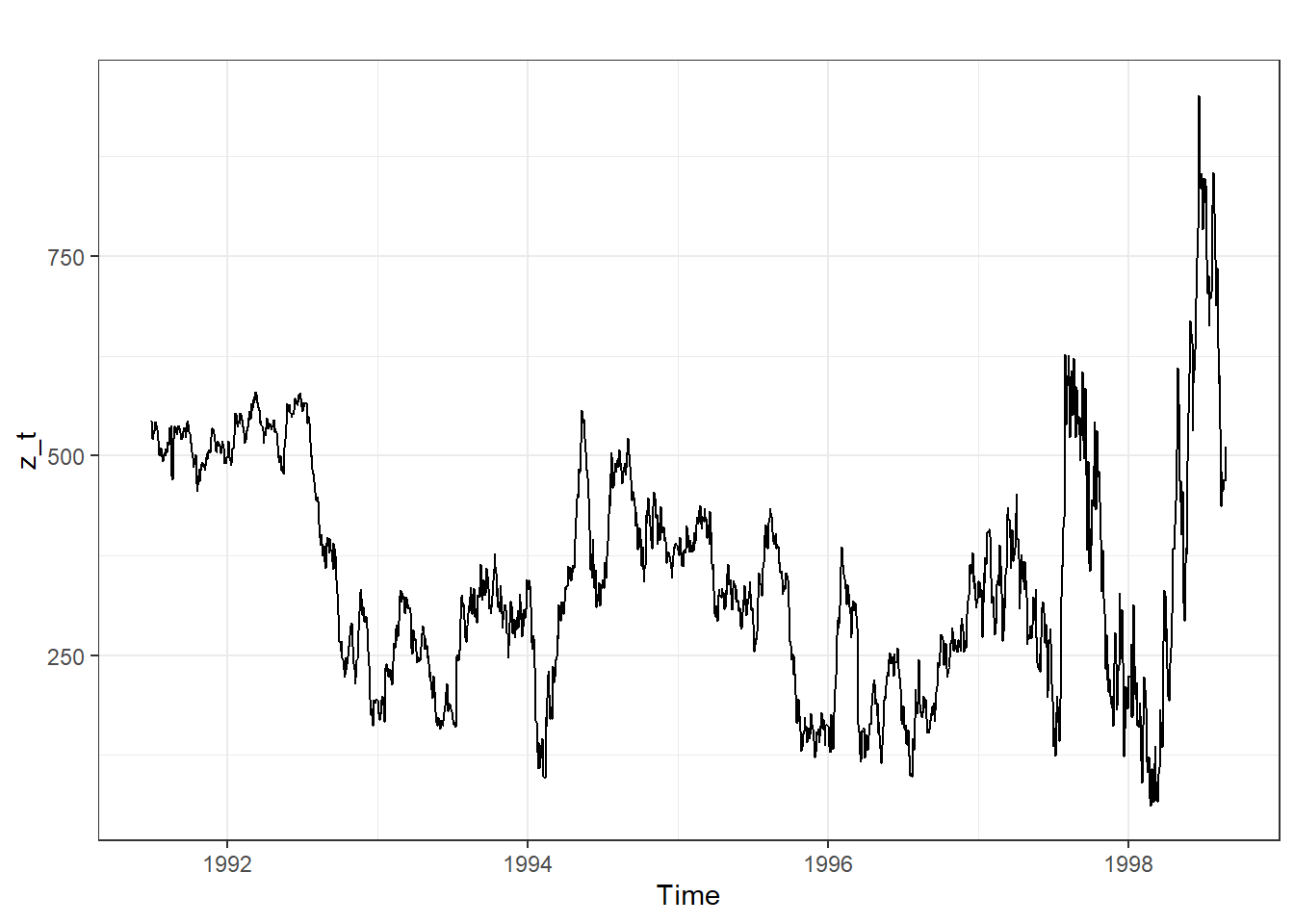
Warning in kpss.test(z_t): p-value smaller than printed p-value
KPSS Test for Level Stationarity
data: z_t
KPSS Level = 2.0542, Truncation lag parameter = 8, p-value = 0.01
Augmented Dickey-Fuller Test
data: z_t
Dickey-Fuller = -3.3581, Lag order = 12, p-value = 0.06065
alternative hypothesis: stationaryEl modelo autorregresivo de rezagos distribuidos o ADL proporciona información sobre el efecto de una serie temporal en el movimiento de otra, al incorporar su propia persistencia mediante autorregresiones.
\[ Y_t = c + \sum_{i=1}^p\alpha_iY_{t-i} + \sum_{j=0}^q\beta_jX_{t-j} + e_t \] En el caso de que dos series estén cointegradas, no es necesario diferenciarlas.
y_t <- EuStockMarkets[,1]
x_t <- EuStockMarkets[,2]
x_t1 <- stats::lag(x_t, 1) #Retardar la independiente 1 periodo
x_t2 <- stats::lag(x_t,2) #Retardar la independiente 2 periodos
w_t = ts.union(x_t, x_t1, x_t2) #Unir las series
w_t = w_t[1:1860,] #Restringir y eliminar las observaciones perdidas
adl <- Arima(y_t, order=c(2,0,0),xreg=w_t) #Modelo ARDL
summary(adl) #ResumenSeries: y_t
Regression with ARIMA(2,0,0) errors
Coefficients:
ar1 ar2 intercept x_t x_t1 x_t2
1.0061 -0.0086 778.6044 -0.0270 -0.0670 0.6159
s.e. 0.0233 0.0233 186.7688 0.0128 0.0128 0.0128
sigma^2 = 458.4: log likelihood = -8328.79
AIC=16671.59 AICc=16671.65 BIC=16710.28
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.3595568 21.37653 14.18575 -0.003301388 0.5421216 0.02581027
ACF1
Training set 5.368272e-05tsframe <- ts.union(y_t, fitted(adl))
autoplot(tsframe) + xlab("") + ylab("") + theme_bw() #Valores estimados por el modelo y serie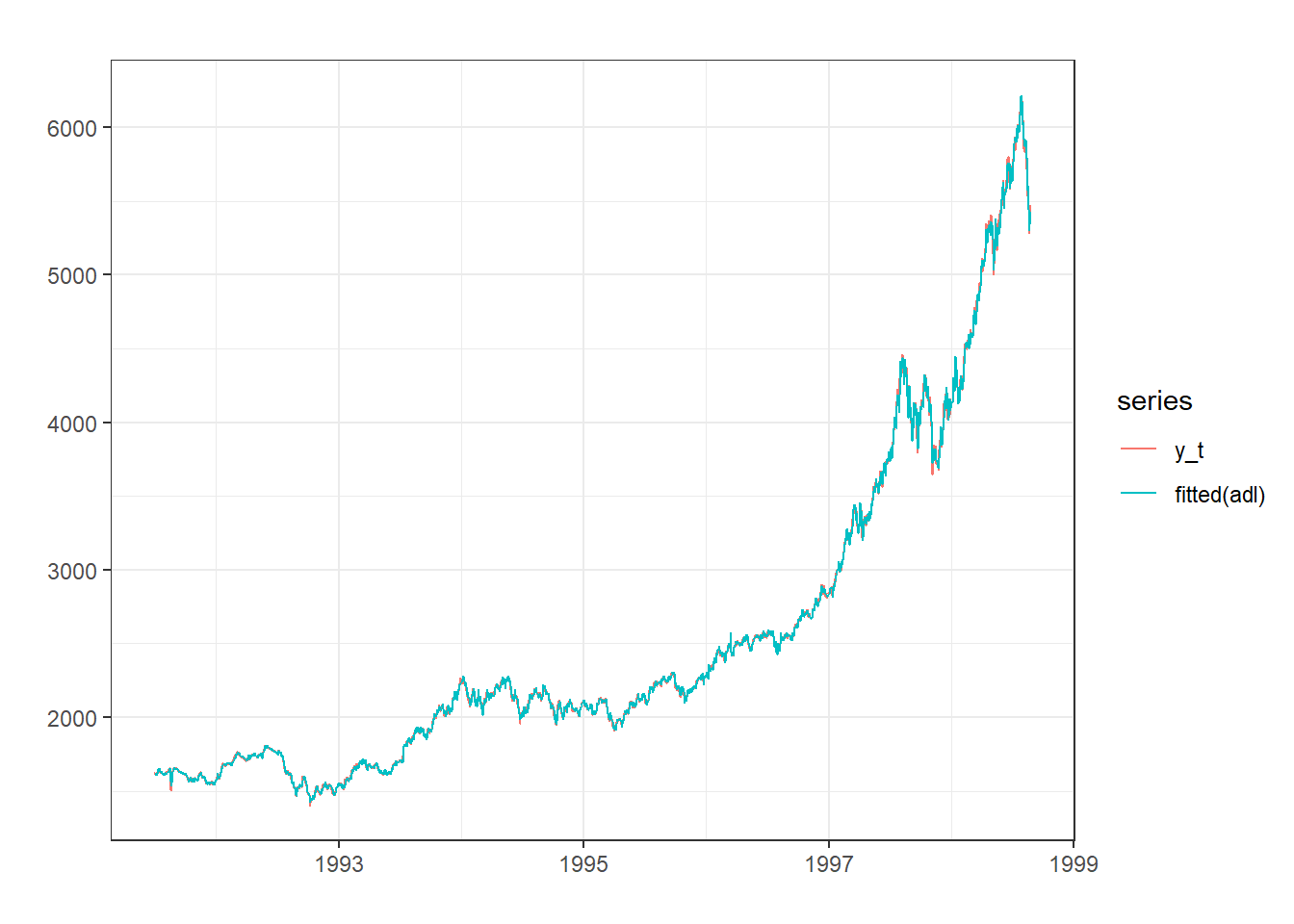
El modelo ADL es extensible a cualquier número de predictores.
Ejercicio: Empleando el conjunto de datos ice.river del paquete tseries, analize la potencial cointegración que pueda existir entre la temperatura y el caudal del río Jokulsa Eystri river.