data("BJsales")
library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
autoplot(BJsales) + theme_classic() #Autoplot de una serie de un indicador adelantado de ventas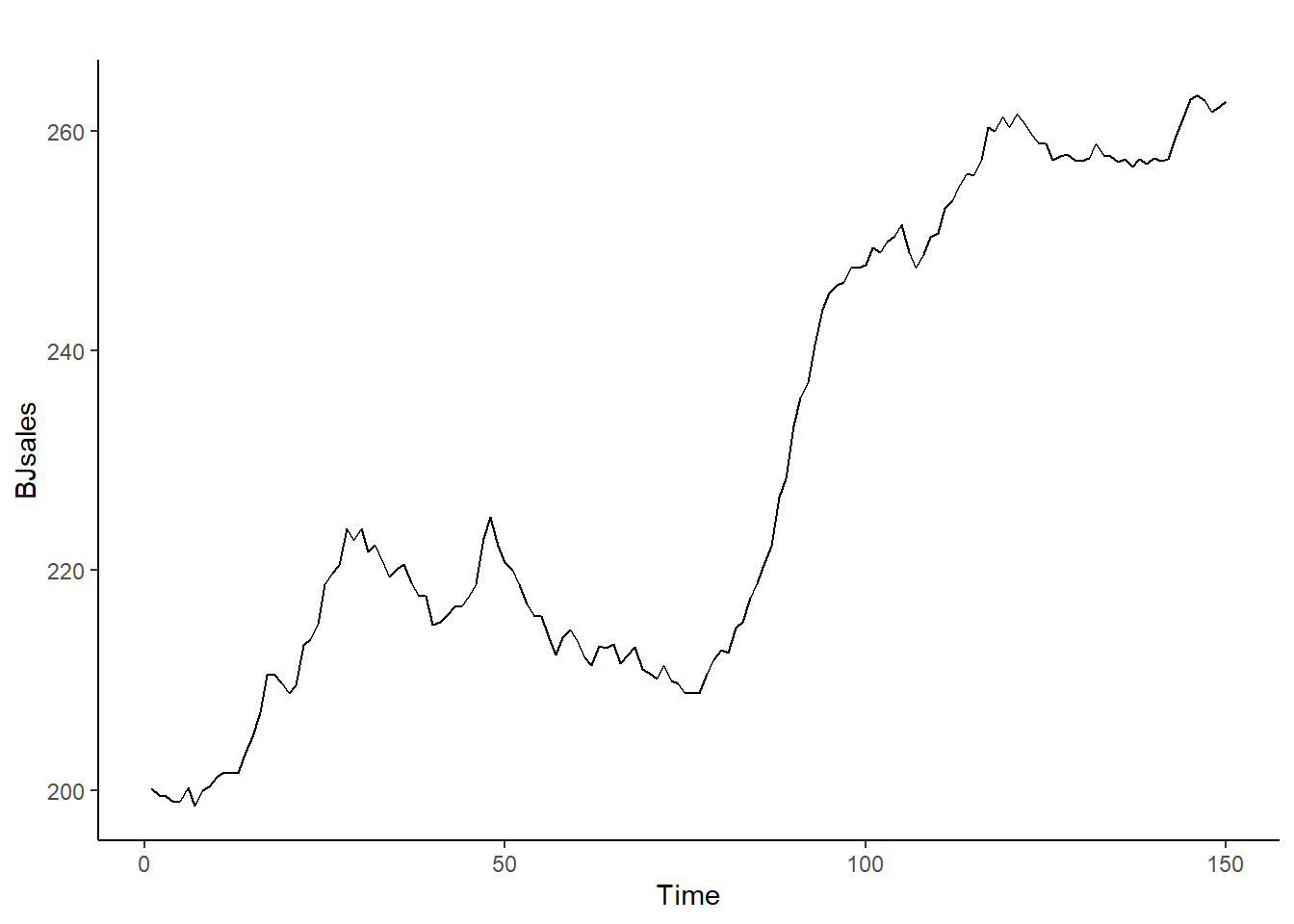
autoplot(log(BJsales)) + theme_classic() #Autoplot de su logaritmo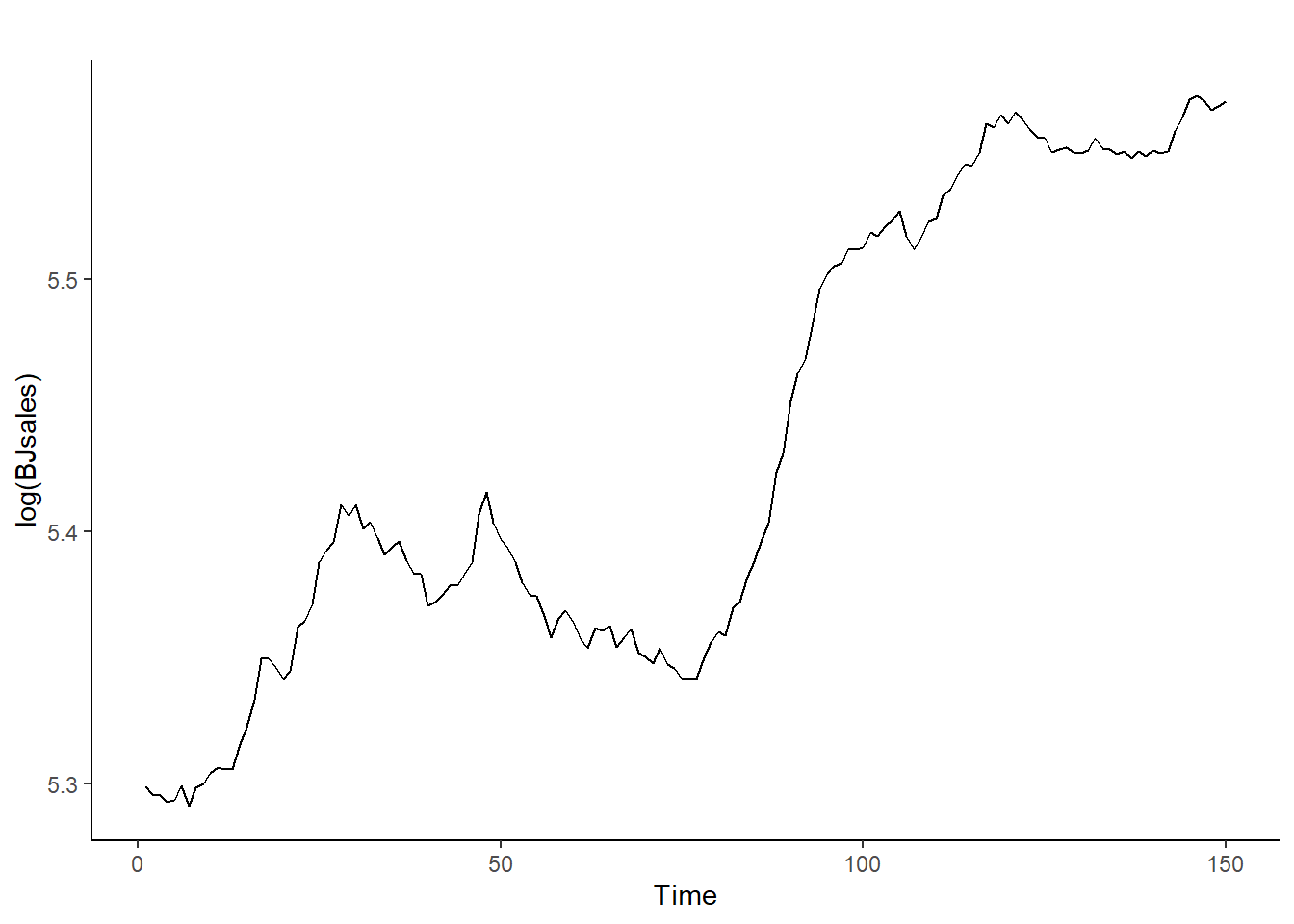
Javier Sánchez García
January 1, 2005
Para realizar un análisis de regresión con series temporales y poder extraer inferencias, primero es necesario que las series temporales sean estacionarias. Para ello, se tienen que dar tres condiciones:
\[ E(y_t) = \mu \tag{1}\]
\[ \sigma^2(y_t)=\sigma^2 \tag{2}\]
\[ \lim_{p \to \infty} E(y_ty_{t-p})=0 \tag{3}\]
que conocemos como estacionareidad en media, varianza y autocorrelación.
La primera condición implica que la serie tiene una media (cualquiera) constante que no depende del tiempo.
La segunda condición implica que la serie tiene una varianza (cualquiera) constante.
La tercera condición implica que la correlación entre la serie y sus valores pasados desaparece conforme pasa el tiempo.
Como hemos visto, la primera condición se consigue con la diferenciación, o bien la inclusión de una tendencia determinística. Veamos que pasa con la de la segunda y tercera condición.
Si una serie no es estacionaria en varianza, se puede conseguir que lo sea mediante la aplicación de logaritmos naturales.
data("BJsales")
library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
autoplot(BJsales) + theme_classic() #Autoplot de una serie de un indicador adelantado de ventas

La clave de la interpretación está en la escala del eje Y. Cuando se representa la serie, esta varía desde 200 a 260. Al aplicar logaritmos naturales, la serie varía desde en el rango [5.3, 5.6], con lo que la varianza será mucho menor. El logaritmo suaviza la varianza de la serie. Sin embargo, la serie no tiene una media constante.
library(forecast, quietly = TRUE)
autoplot(diff(BJsales,1)) + theme_classic() #Autoplot de las primeras diferencias de la serie.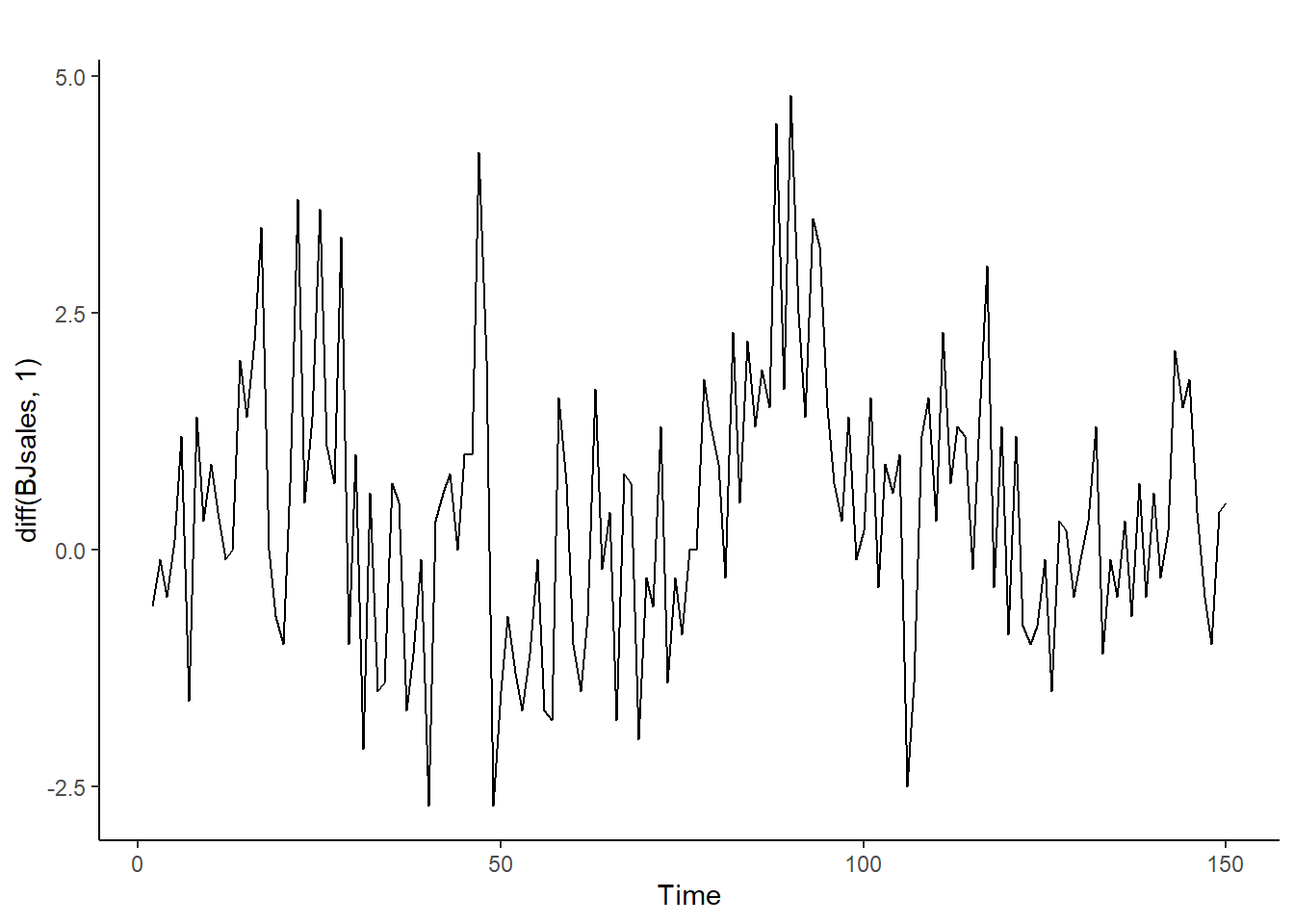
autoplot(diff(log(BJsales)),1) + theme_classic() #Autoplot del logaritmo de las primeras diferencias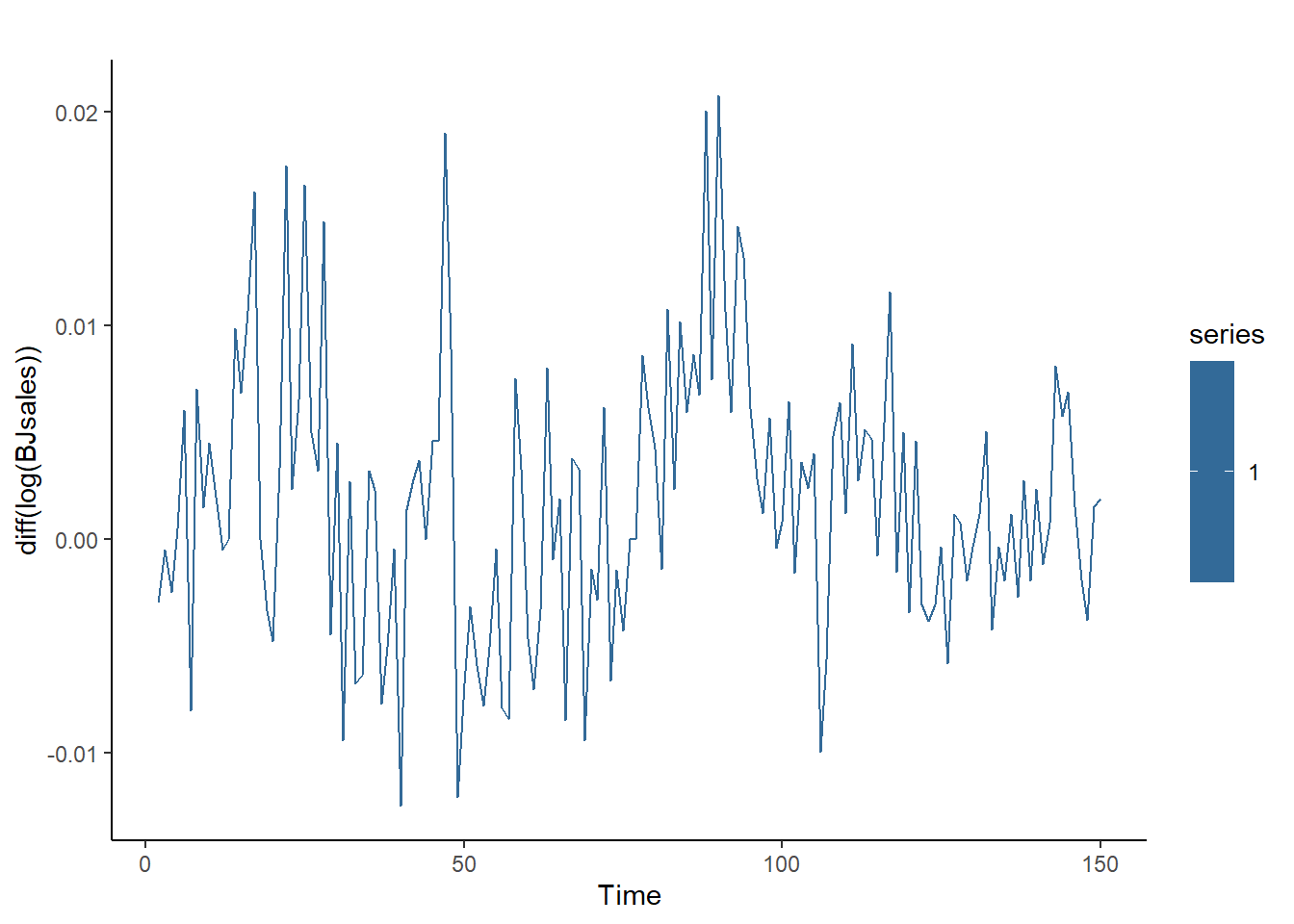
Al aplicar primeras diferencias, se eliminan las tendencias y la media es constante. Si antes se aplican logaritmos, la serie será estacionaria en media y varianza, como se aprecia al analizar el eje y de las gráficas.
Para medir el grado de autocorrelación de orden \(r\) una serie, se emplea el coeficiente de autocorrelación (\(\rho\))
\[ \rho_r = \frac{\sum_{t=r+1}^{n}(y_t-\bar{y})(y_{t-r}-\bar{y})}{\sum_{t=1}^{n}(y_t - \bar{y})^2} \]
siendo \(n\) el tamaño de la serie temporal.
Normalmente, este coeficiente se representa para los \(r\) retardos en un gráfico de autocorrelación o correlograma:
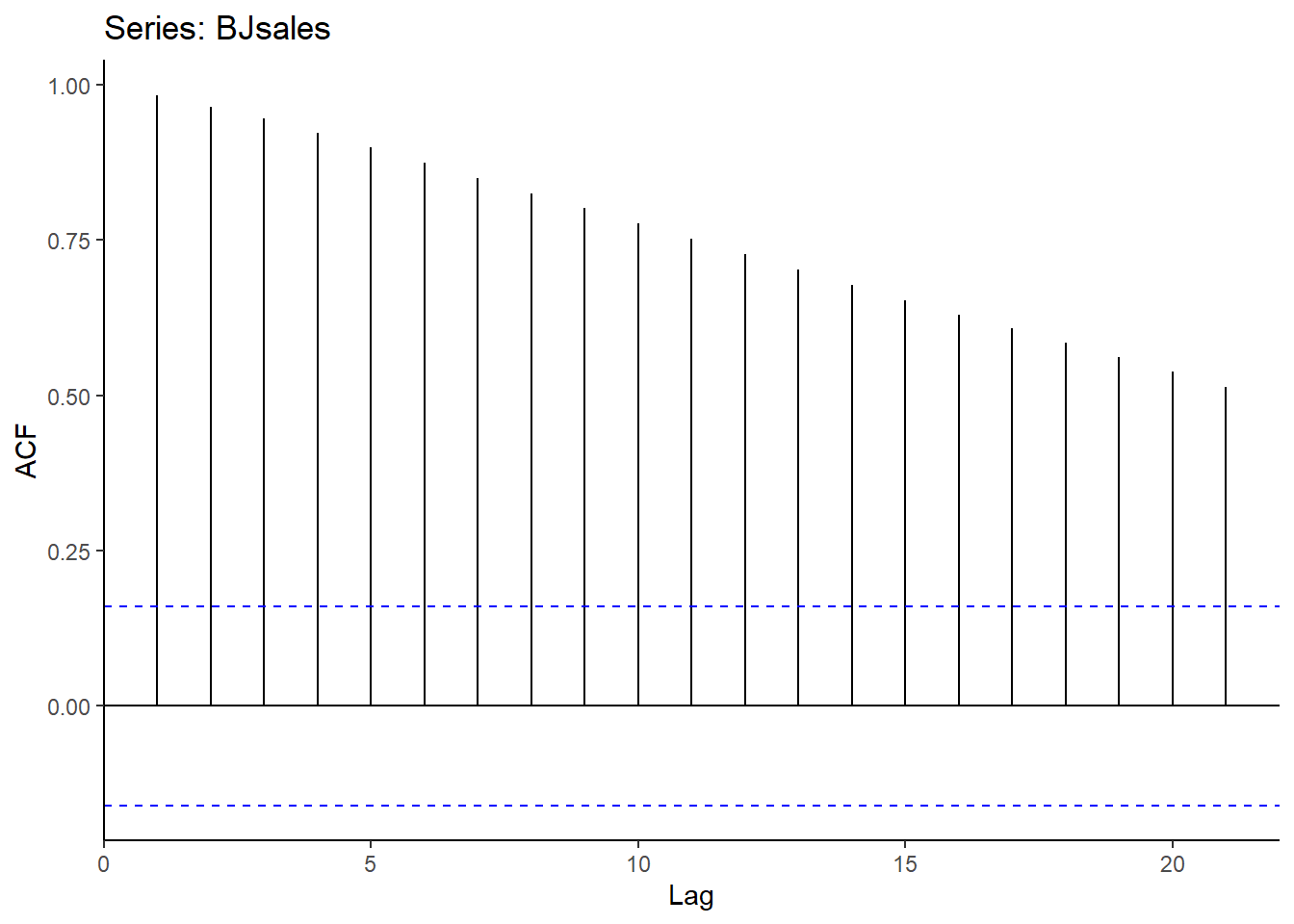
ggAcf(diff(log(BJsales),1)) + theme_classic() #Correlograma del indicador de ventas log-diferenciado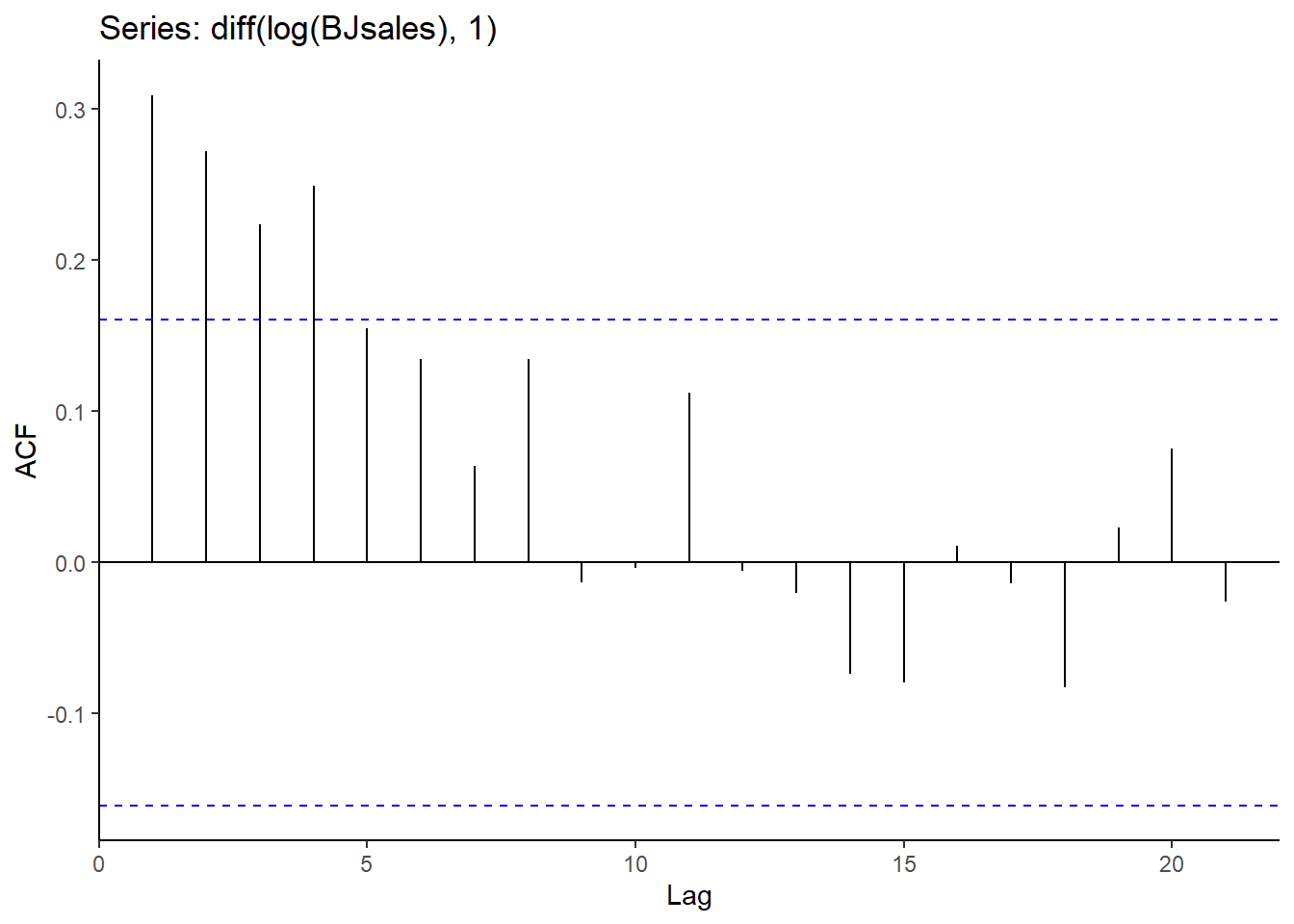
Es evidente que la serie log-diferenciada está mucho menos autocorrelacionada conforme avanza el tiempo.
Aunque un análisis visual siempre arroja información sobre si una serie es o no estacionaria, existen test estadísticos que permiten contrastarlo formalmente. Es el caso del contraste KPSS.
Contraste KPSS:
Hipótesis nula (H0): La serie es estacionaria.
Hipótesis alternativa. (H1): La serie no es estacionaria.
library(tseries, quietly=TRUE)
kpss.test(BJsales.lead) #Test para serie no estacionaria (se rechaza nula)
KPSS Test for Level Stationarity
data: BJsales.lead
KPSS Level = 2.556, Truncation lag parameter = 4, p-value = 0.01
KPSS Test for Level Stationarity
data: diff(log(BJsales), 1)
KPSS Level = 0.12482, Truncation lag parameter = 4, p-value = 0.1Ejercicio: Cargue, inspeccione y analize la estacionareidad en media, varianza y autocorrelación de la serie LakeHuron. Si no es estacionaria, tránsformela para que lo sea. Contraste formalmente la estacionareidad de la serie original, y de la serie transformada.