library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
data("gold")
gold1 <- ts(gold, start=c(1985,1), end=c(1989,03), frequency = 365)
autoplot(gold1) +geom_smooth(lwd=0.5) + xlab("") + ylab("") + theme_classic()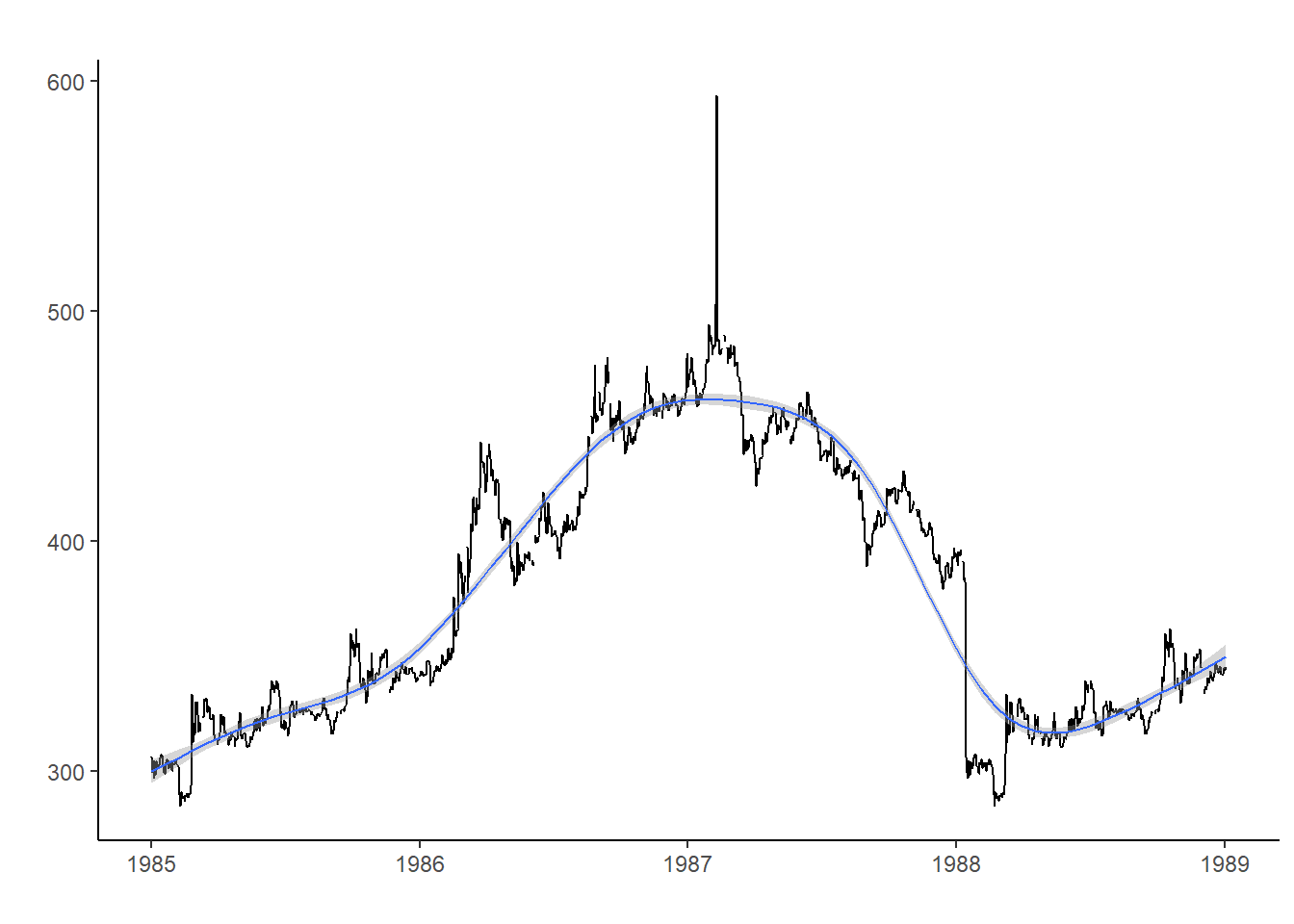
Javier Sánchez García
January 1, 2004
Además del componente estacional, y de las tendencias que se pueden ajustar como una función del paso del tiempo, existen otro tipo de tendencias. Una tendencia estocástica define la trayectoria a largo plazo de una serie, pero de forma aleatoria.
library(forecast, quietly=TRUE)
library(ggplot2, quietly=TRUE)
data("gold")
gold1 <- ts(gold, start=c(1985,1), end=c(1989,03), frequency = 365)
autoplot(gold1) +geom_smooth(lwd=0.5) + xlab("") + ylab("") + theme_classic()
En la figura anterior, la tendencia ajustada con geom_smooth() no captura completamente el comportamiento de la serie, que es mucho más errático que la función del tiempo. Por ejemplo, entre 1987, el precio sube y baja de forma mucha mas continua de lo que ajusta la línea. Esto es debido a que la línea constituye una tendencia determinística (que crece o decrece dependiendo de una función conocida), mientras que la serie temporal se ajusta a una tendencia estocástica (que crece o decrece sujeta a la aleatoriedad).
De manera que:
\[ y_t= f(t) \]
constituye una serie dependiente de tendencia determinística, y
\[ y_t= f(t) + \epsilon_t \]
constituye una serie dependiente de una tendencia estocástica. El componente \(\epsilon_t\) es aleatorio o impredecible, y hace que la serie se desvíe de forma aleatoria de su trayectoria predecible.
Para eliminar una tendencia estocástica, basta con realizar primeras diferencias de la serie temporal. Para ello, primero hay que retardar la variable.
y = c(2, 3.5, 6, 8, 9, 10) #Generación de datos
y_t = ts(y, start=2000) #Asignación serie temporal
y_t1 = lag(y_t, 1) #Retardar la variable
y_tTime Series:
Start = 2000
End = 2005
Frequency = 1
[1] 2.0 3.5 6.0 8.0 9.0 10.0Time Series:
Start = 1999
End = 2004
Frequency = 1
[1] 2.0 3.5 6.0 8.0 9.0 10.0| \(t\) | \(y_t\) | \(y_{t-1}\) |
|---|---|---|
| 2000 | 2 | 3.5 |
| 2001 | 3.5 | 6 |
| 2002 | 6 | 8 |
Es decir, en el año 2001, \(y_t\) tiene valor 3.5, luego \(y_{t-1}\) tendrá dicho valor en el año 2000. Toda la variable se retarda 1 periodo.
Las primeras diferencias de la serie \(y_t\), denotadas como \(\Delta y_t\), se calculan:
\[ \Delta y_t = y_t - y_{t-1} \]
En caso de que la tendencia no se elimine, este proceso se puede iterar al orden \(k\), donde la diferenciación toma la forma:
\[ \Delta^k y_t = y_t - y_{t-k} \]
En el caso del ejemplo anterior:
goldt1 <- diff(gold1, 1) #Comando para primeras diferencias
autoplot(goldt1) + xlab("") + ylab("") + theme_classic() #Representación de la serie diferenciada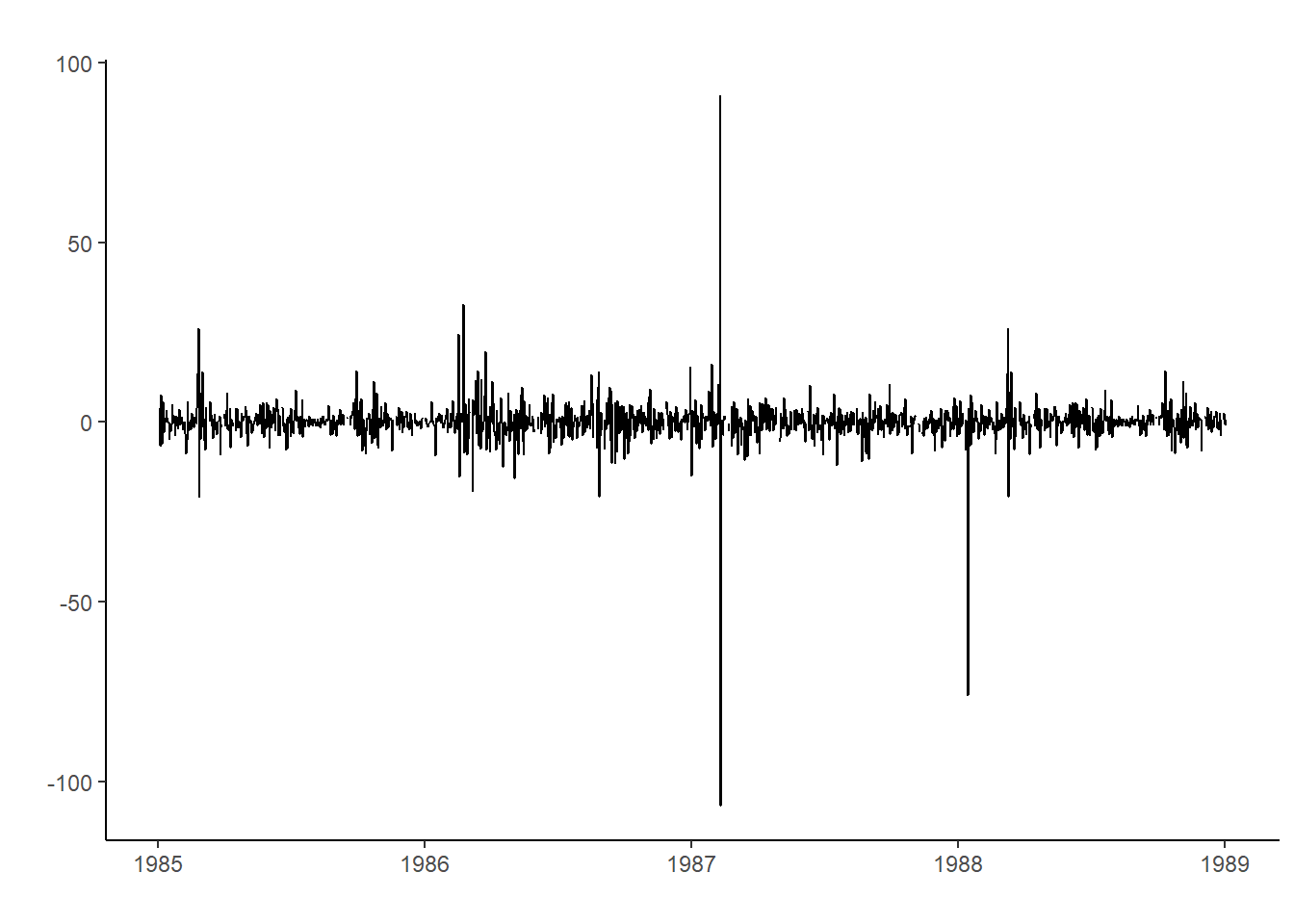
Donde lo que se representa ahora es la variación de la serie. Este proceso elimina la tendencia estocástica, puesto que la media ahora es constante.
Este proceso también se puede aplicar para eliminar la tendencia estacional. Si la frecuencia de los datos es \(s\) , entonces se puede diferenciar en el orden \(s\) para eliminar el componente estacional.
Es decir, la serie:
\[ \Delta^s y_t = y_t - y_{t-s} \]
estará libre del componente estacional.
data("AirPassengers") #Datos de pasajeros mensuales durante 20 años de una compañía aérea.
forecast::autoplot(AirPassengers) + theme_classic() #Serie con componente estacional.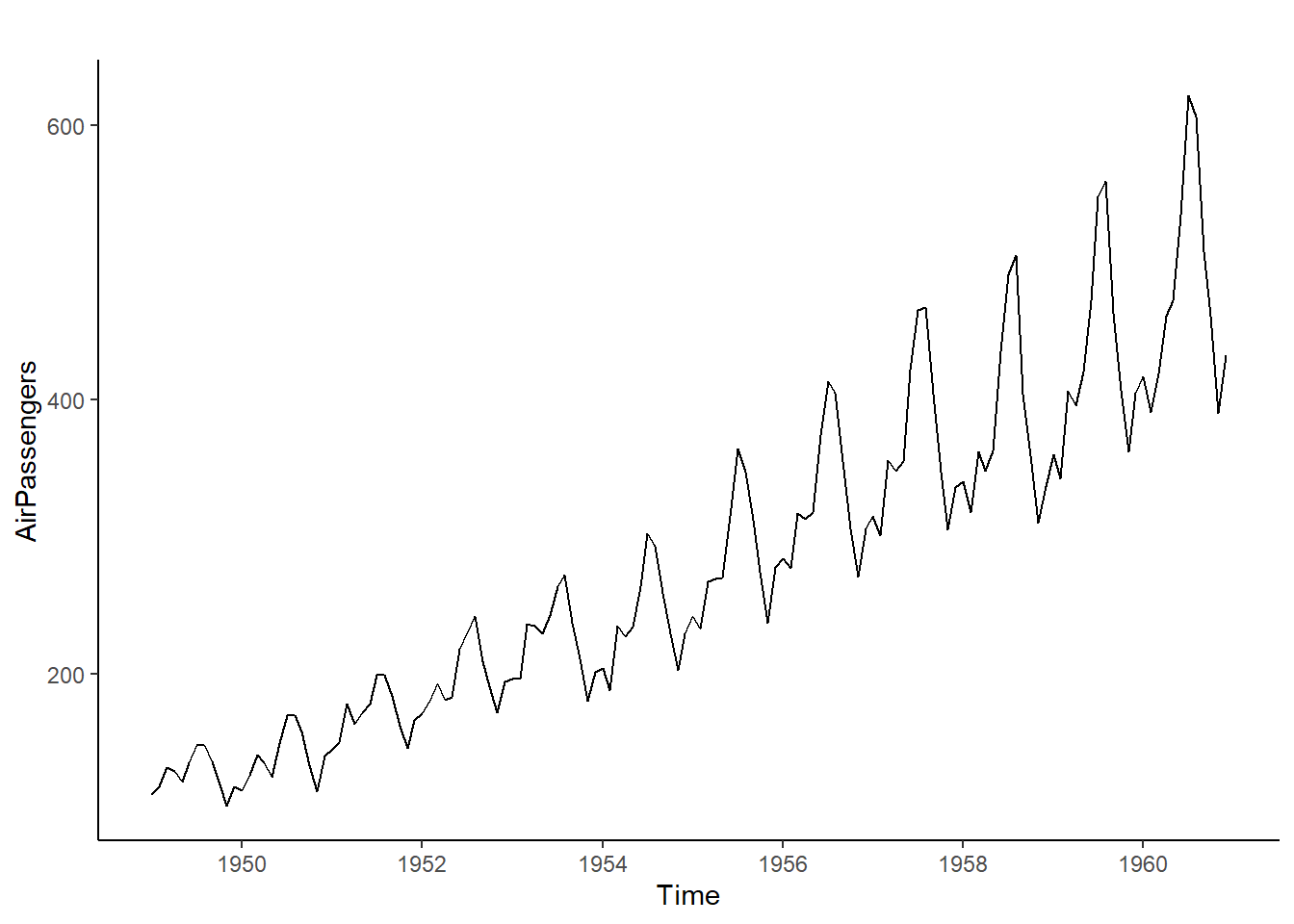
Claramente se tienen más pasajeros en los meses de vacaciones.
pasajeros_noestacional <- diff(AirPassengers, 12) #diferencias estacionales
forecast::autoplot(pasajeros_noestacional) + theme_classic() #Serie sin componente estacional.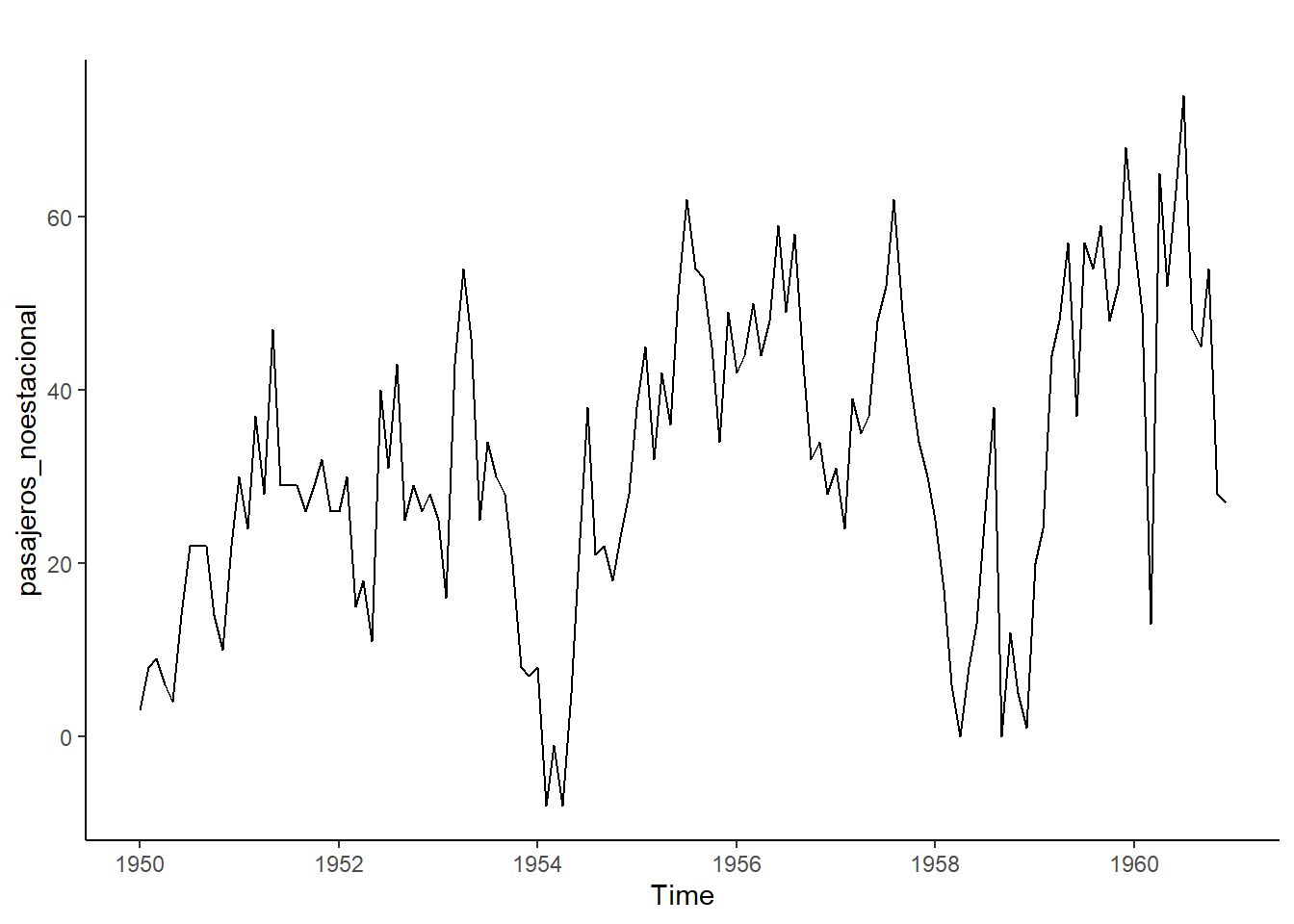
Como alternativa, se pueden emplear \(1, \ldots, s\) variables ficticias para capturar el componente estacional, y después restar dicho efecto a la serie, para conseguir una serie desestacionalizada.